Pagerank的简单理解

作为全球最大最好用的搜索引擎Google，大家都想知道它使用的是什么算法把网页搜索做的那么流畅。当然我们无从得知其具体做法，但其中的核心思想还是可以去窥探一二的。

如果说百度更懂中文，那么谷歌就更懂我。当然，大家都想要一个更懂自己的搜索引擎。那么谷歌是如何做到更懂你的呢，其中最著名的算法就是佩奇排名了(PageRank)。第一次听到这个名词的时候以为这个 Page 就是网页的意思，后来才知道这个算法是谷歌创始人之一的拉里·佩奇(Larry Page)来命名的。这个算法的主要作用就是分析网页的相关性和重要性，下面我们就一起来看一看其中的核心思想。

首先我们假设有四个网页，刚开始他们都没有链接到任何其他网页，也没有被其他网页链接，如下图所示。那么所有网页的rank值记为 $PR()=0$，而所有网页连接到其他网页的概率也为0，而总值我们设置为 1 。

好了，那如果现在的链接和被链接情况如下图所示的话，我们就可以用一个矩阵来表示它们之间的关系，其中列表示该网页连接到其他网页的概率，行则表示其他网页链接到此网页的情况。

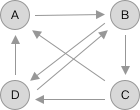
从图中可以看出 A 页面把唯一的链接给了 B ，而 B 页面同时链接了 D 和 C ，C 页面同时链接了 A 和 D，D 页面则同时链接了 B 和 A。 如果我们把每一个链接都打分，然后每一个页面链接出去的分数总和为 1 的话，就得到如下图所示：

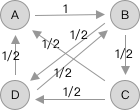
那么用矩阵表示如下：

\begin{align} \begin{bmatrix} 0 & 0 & 1/2 & 1/2 \\ 1 & 0 & 0 & 1/2 \\ 0 & 1/2 & 0 & 0 \\ 0 & 1/2 & 1/2 & 0 \end{bmatrix} \end{align}

从矩阵表示中可以看出，每一列的和都为 1，表示每个网页链接到其他网页的总概率为 1。也就是说如果你现在在网页 B，那么你有 50% 的概率连接到网页 C 和 D。

那么，我们如何计算每一个网页的 $PR$ 值的。到此我们只有了一个表示网页之间互相链接情况的矩阵，那么还需要一个初始的网页打分矩阵，然后就可以去计算更新各个网页的 $PR$ 值了。这里为了讨论的简单，用如下 $R_0$ 矩阵来表示每个网页初始的受欢迎程度:

\begin{align} \begin{bmatrix} 0.25 \\ 0.25 \\ 0.25 \\ 0.25 \end{bmatrix} \end{align}

然后使用链接矩阵和初始 $R_0$ 矩阵相成就可以得到第一次循环的 $R_1$ 矩阵：

\begin{align} \begin{bmatrix} 0 & 0 & 1/2 & 1/2 \\ 1 & 0 & 0 & 1/2 \\ 0 & 1/2 & 0 & 0 \\ 0 & 1/2 & 1/2 & 0 \end{bmatrix} \begin{bmatrix} 0.25 \\ 0.25 \\ 0.25 \\ 0.25 \end{bmatrix} = \begin{bmatrix} 0.25 \\ 0.375 \\ 0.125 \\ 0.25 \end{bmatrix} \end{align}

从中我们看出，网页 B 打了最高的分数，因为有两个网页链接给了它，而且其中一个网页把给了它百分百的链接。而网页 C 是最低分，它的唯一链接来自于 B，而 B 同样也链接给了 D，网页 A 和 D 的分数相同都是初始值 0.25。现在我们把 $R_0=R_1$，再一次进行上面的循环，然后再把得到的 $R_1$ 赋值给 $R_0$ … 这样一直循环下去就会看到 $R_0$ 会逼近一个值。如果我们把初始的链接矩阵用 $A$ 来表示，那么这个过程可以表示为如下极限：

\begin{align} \lim\limits_{n\rightarrow\infty}{A^nR_0}= \begin{bmatrix} 0.217 \\ 0.348 \\ 0.174 \\ 0.261 \end{bmatrix} \end{align}

从中我们可以看出 网页 A 虽然和 网页 D 有相同的链接数，但他们来自不同质量的网页，网页 D 其中一个链接是网页 B 给的，而网页 B 是 $PR$ 最高也就是质量最高的网页。因此不仅仅是链接数决定了这个网页的打分，更重要的是链接的质量。即使你的网页被很多网页所链接，并不代表它被谷歌承认的概率的高一点，如果都是垃圾链接的话可能就一文不值了。

个人的一点理解，也只能当做饭后的谈资或者一点回味了。